Since the response time of MR dampers is usually in the order of a few milliseconds, one may use MR dampers for advanced control system design. Sliding mode control is a popular control methodology wherein one uses a switching on-off control in many electromechanical systems. There are quite a few advantages in using sliding mode control including reduction of system order and increase in system robustness. MR dampers can also be used to achieve sliding mode control in vibrating systems like seat suspensions, vehicle suspensions, washing machines and prosthetic devices.
1. One degree of Freedom System
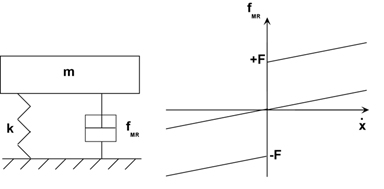
Fig 1 - A simple mass-spring-MR damper system
 |
(1)
|
', one may ensure that the sliding mode 's = 0' exists, i.e. '
' by choosing a control as shown in equation (2). |
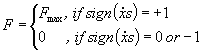(2)
|
By further analysis one may easily prove that this enforces the sliding mode. The following figures (2 - 5) shows an initial condition (
) response to the SDOF system with '
'.
 |
|
Figure 1. Positon vs Time
|
 |
|
Figure 2. Velocity vs Time
|
 |
|
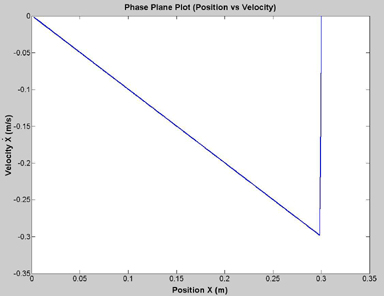
Figure 4. Phase Plane Plot (Position vs Velocity)
|
 |
|
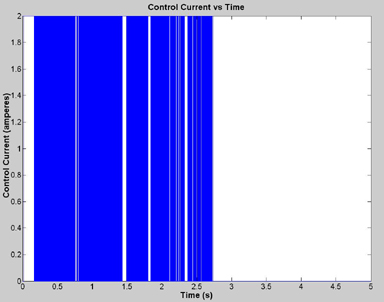
Figure 5. Control Current vs Time
|
A simple experimental setup was designed and run to compare the controlled response with the uncontrolled system. In the experiment the mass was given a vibrating sinusoidal force input using the MTS actuator and the spring. The figures 6 to 8 show the experimental setup and the experimental results.
Figure 7. Frequency response amplitude with and without sliding mode control
Figure 8. Mass Displacement vs Time Plot
2. Two degree of Freedom System
The same strategy may be extended to a two degree of freedom system also. Consider a system shown in figure 9.
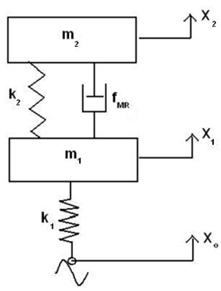
Figure 9. Two DOF system using MR Damper
 |
(3)
|
 |
(4)
|
The dynamic state-space equation for the system may be written as follows
 |
(5)
|
 |
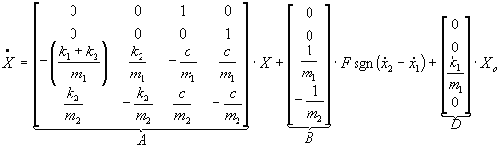(6)
|
' where G = 
. The sliding mode may be enforced (
) by using the control law as shown in equation (7).
 |
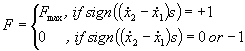(7)
|